This notebook is part of a set of examples for teaching Bayesian inference methods and probabilistic programming, using the numpyro library.
import io
import arviz as az
import jax
import matplotlib.pyplot as plt
import numpy as np
import numpyro
import numpyro.distributions as dist
import numpyro.infer
import pandas as pd
from IPython.display import display
from scipy.special import expitFIGSIZE = (6.4, 4.8)
TEXTSIZE = 10rng_key = jax.random.PRNGKey(1)The data consists of the initial and final numbers of surviving reed frog tadpoles that were held for some duration in a set of tanks, under similar conditions, except that some were exposed to predators (dragonflies). In this example, we will model the tadpoles’ probability for survival in the different tanks, taking into account the effect of predators, as well as other inter-tank variability.
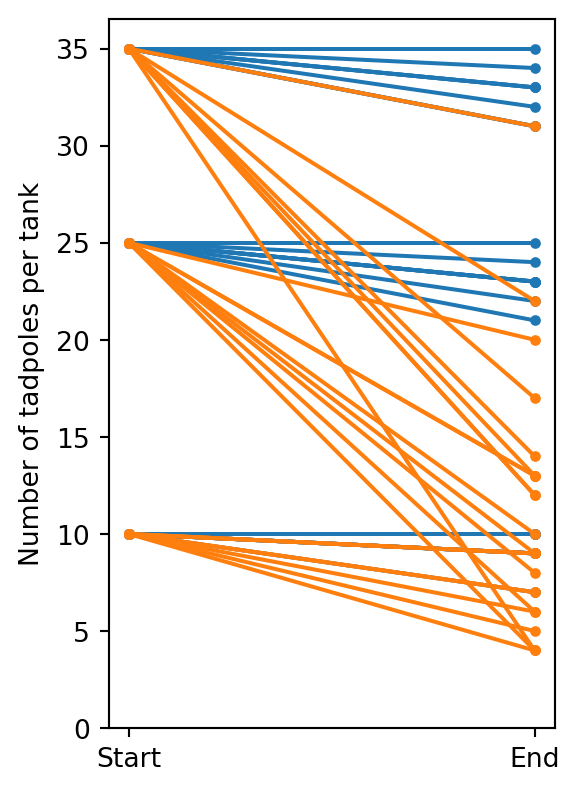
csv = """
num_start,has_predators,is_large,num_end
10,0,1,9
10,0,1,10
10,0,1,7
10,0,1,10
10,0,0,9
10,0,0,9
10,0,0,10
10,0,0,9
10,1,1,4
10,1,1,9
10,1,1,7
10,1,1,6
10,1,0,7
10,1,0,5
10,1,0,9
10,1,0,9
25,0,1,24
25,0,1,23
25,0,1,22
25,0,1,25
25,0,0,23
25,0,0,23
25,0,0,23
25,0,0,21
25,1,1,6
25,1,1,13
25,1,1,4
25,1,1,9
25,1,0,13
25,1,0,20
25,1,0,8
25,1,0,10
35,0,1,34
35,0,1,33
35,0,1,33
35,0,1,31
35,0,0,31
35,0,0,35
35,0,0,33
35,0,0,32
35,1,1,4
35,1,1,12
35,1,1,13
35,1,1,14
35,1,0,22
35,1,0,12
35,1,0,31
35,1,0,17
"""
data = pd.read_csv(io.StringIO(csv))
data = data.drop(columns=["is_large"])def plot_data(ax=None):
if ax is None:
_, ax = plt.subplots(figsize=(3, FIGSIZE[1]))
x = [0, 1]
for i, d in data.iterrows():
y = [d["num_start"], d["num_end"]]
ax.plot(x, y, c="C1" if d["has_predators"] else "C0", marker=".")
ax.set_xticks(x, labels=["Start", "End"])
ax.set_ylim(0, None)
ax.set_ylabel("Number of tadpoles per tank")
return ax
plot_data()
plt.show()
| num_start | has_predators | num_end | |
|---|---|---|---|
| 0 | 10 | 0 | 9 |
| 1 | 10 | 0 | 10 |
| 2 | 10 | 0 | 7 |
| 3 | 10 | 0 | 10 |
| 4 | 10 | 0 | 9 |
| ... | ... | ... | ... |
| 43 | 35 | 1 | 14 |
| 44 | 35 | 1 | 22 |
| 45 | 35 | 1 | 12 |
| 46 | 35 | 1 | 31 |
| 47 | 35 | 1 | 17 |
48 rows × 3 columns
For each tank \(i\), let’s express the tadpoles’ survival probability as \(p_i=\text{logit}(\alpha_i)\), where the log-odds \(\alpha_i=\alpha_{t,i}+\alpha_p\) have a tank-dependent term \(\alpha_{t,i}\), and a predator-dependent term \(\alpha_p\) that is zero in the absence of predators.
def model(df):
num_start = numpyro.param("num_start", df["num_start"].values)
num_end = numpyro.param("num_end", df["num_end"].values)
has_predators = numpyro.param("has_predators", df["has_predators"].values)
mean = numpyro.sample("mean", dist.Normal(0, 1.5))
sigma = numpyro.sample("sigma", dist.Exponential(1))
alpha_p = numpyro.sample("alpha_p", dist.Normal(0, 0.5))
with numpyro.plate("tank", len(data)):
alpha_t = numpyro.sample("alpha_t", dist.Normal(mean, sigma))
alpha = numpyro.deterministic("alpha", alpha_t + alpha_p * has_predators)
numpyro.sample("num_obs", dist.Binomial(num_start, logits=alpha), obs=num_end)numpyro.render_model(
model=model,
model_args=(data,),
render_params=True,
render_distributions=True,
)
sampler = numpyro.infer.MCMC(
sampler=numpyro.infer.NUTS(model),
num_warmup=2000,
num_samples=10000,
num_chains=4,
progress_bar=False,
)rng_key, _rng_key = jax.random.split(rng_key)
sampler.run(_rng_key, data)inf_data = az.from_numpyro(sampler)
inf_data.posterior["p"] = expit(inf_data.posterior["alpha"])def plot_trace(ax=None):
return az.plot_trace(
data=inf_data,
figsize=(FIGSIZE[0], 4 * 2),
var_names=["~alpha", "~p"],
axes=ax,
)
plot_trace()
plt.tight_layout()
plt.show()
az.summary(inf_data, kind="all", var_names=["~alpha_t", "~alpha", "~p"])| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha_p | -1.823 | 0.304 | -2.405 | -1.262 | 0.004 | 0.003 | 6097.0 | 9477.0 | 1.0 |
| mean | 2.194 | 0.230 | 1.767 | 2.633 | 0.002 | 0.002 | 9094.0 | 15609.0 | 1.0 |
| sigma | 0.913 | 0.168 | 0.613 | 1.235 | 0.002 | 0.001 | 11742.0 | 20416.0 | 1.0 |
def plot_forest(ax=None):
_ax = az.plot_forest(
data=inf_data,
figsize=(FIGSIZE[0], 0.2 * len(data)),
var_names=["p"],
combined=True,
colors="black",
markersize=10 * 0.75,
textsize=TEXTSIZE,
ax=ax,
)
ax = _ax[0]
dy = 0.825
y = np.arange(len(data)) * dy
y = y[::-1]
mask = data["has_predators"].values == 1
post_mean = az.extract(inf_data).mean("sample")
p_m = expit(float(post_mean["mean"]) + mask * float(post_mean["alpha_p"]))
ax.plot(p_m, y, ls="none", marker="|", ms=10, c="black")
p_t = expit(post_mean["alpha_t"])
ax.plot(p_t[mask], y[mask], ls="none", marker=".", ms=10, mfc="none", mec="black")
p_obs = data["num_end"] / data["num_start"]
ax.plot(p_obs, y, ls="none", marker="D", ms=5, mfc="1", mec="0")
colors = np.where(mask, "C1", "C0")
for i, d in data.iterrows():
y1, y2 = y[i] - dy / 2, y[i] + dy / 2
ax.fill_between([0, 1], y1, y2, color=colors[i], ec="none", alpha=0.1)
ax.axhline(np.mean(y[15:17]), c="black", ls="dashed")
ax.axhline(np.mean(y[31:33]), c="black", ls="dashed")
ax.set_yticks([])
ax.set_xlabel(r"$p$")
ax.set_ylim(-dy / 2, np.max(y) + dy / 2)
return ax
plot_forest()
plt.show()
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.20.0
arviz : 0.17.0
numpy : 1.26.3
pandas : 2.1.4
matplotlib: 3.8.2
numpyro : 0.13.2
jax : 0.4.23