The Galaxy Case

This notebook is part of a set of examples for teaching Bayesian inference methods and probabilistic programming, using the numpyro library.

Imports

import io

import arviz as az
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import numpyro
import numpyro.distributions as dist
import numpyro.handlers
import numpyro.infer
import pandas as pd
import scipy.stats

from arviz.labels import MapLabeller
from IPython.display import display
from numpyro.infer.reparam import LocScaleReparam

Constants

FIGSIZE = (6.4, 4.8)
TEXTSIZE = 10

MARKER_STYLE = {"marker": "o", "ls": "none", "lw": 2, "capsize": 4}
INDICATOR_STYLE = {"c": "gray", "ls": "dotted"}

LABELLER = MapLabeller({"sigma": r"$\sigma$ (km/s)", "v0": r"$v_0$ (km/s)"})

RNG Setup

rng_key = jax.random.PRNGKey(1)

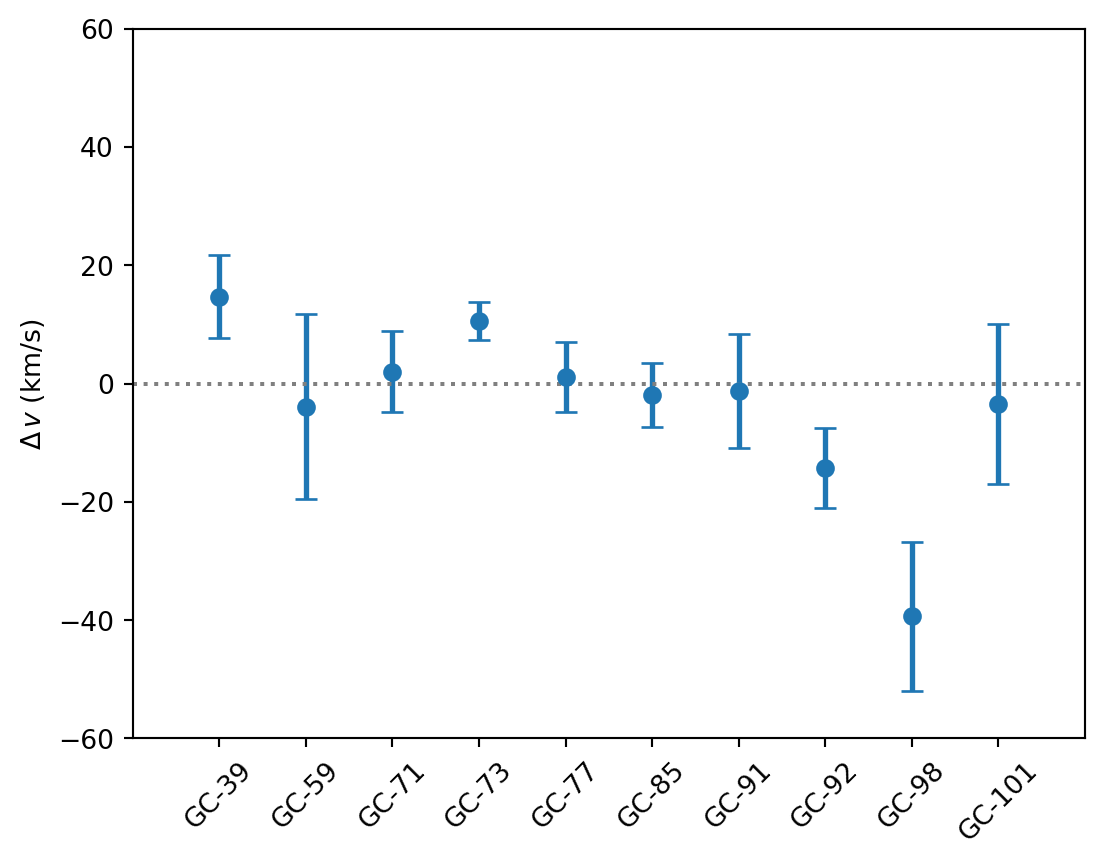
The data consists of radial (line-of-sight) velocities measured for ten globular-cluster-like objects in the ultra-diffuse galaxy NGC1052–DF2. In this example, we will estimate a velocity dispersion from these measurements, taking into account the given measurement uncertainties. From this velocity dispersion, it is possible to estimate the total mass of the galaxy halo, and thus its dark matter fraction (by comparison with its independently estimated stellar mass).

Data

Data

csv = """
name,v,v_err
GC-39,14.728960068829865,7.046858966028704
GC-59,-3.8926505316836715,15.641403662859219
GC-71,2.0484049489377583,6.883925810744802
GC-73,10.576494786228665,3.2586631056780107
GC-77,1.1716309895635035,5.906326879041401
GC-85,-1.9077877208626857,5.3767941243687225
GC-91,-1.2121402228903977,9.69434349499684
GC-92,-14.32028284765569,6.761636322084257
GC-98,-39.335899515592,12.586586245681328
GC-101,-3.3753512069869345,13.523451888563756
"""

data = pd.read_csv(io.StringIO(csv))

Figure

def plot_data(ax=None):
    if ax is None:
        _, ax = plt.subplots(figsize=FIGSIZE)

    ax.errorbar(x=data.index, y=data["v"], yerr=data["v_err"], **MARKER_STYLE)
    ax.axhline(0, **INDICATOR_STYLE)

    ax.set_xticks(data.index, labels=data["name"], rotation=45)
    ax.set_ylabel(r"$\Delta\,v$ (km/s)")
    ax.set_xlim(-1, 10)
    ax.set_ylim(-60, 60)
    return ax


plot_data()
plt.show()

Figure 1: The radial velocities of ten globular-cluster-like objects in NGC1052–DF2.

	name	v	v_err
0	GC-39	14.728960	7.046859
1	GC-59	-3.892651	15.641404
2	GC-71	2.048405	6.883926
3	GC-73	10.576495	3.258663
4	GC-77	1.171631	5.906327
5	GC-85	-1.907788	5.376794
6	GC-91	-1.212140	9.694343
7	GC-92	-14.320283	6.761636
8	GC-98	-39.335900	12.586586
9	GC-101	-3.375351	13.523452

Model

def model(df):
    v_meas = numpyro.param("v_meas", df["v"].values)
    v_err = numpyro.param("v_err", df["v_err"].values)

    v0 = numpyro.sample("v0", dist.Uniform(-50, 50))
    sigma = jnp.exp(numpyro.sample("log_sigma", dist.Uniform(np.log(0.5), np.log(50))))

    with numpyro.plate("data", len(df)):
        with numpyro.handlers.reparam(config={"v": LocScaleReparam(0)}):
            v = numpyro.sample("v", dist.Normal(v0, sigma))
        numpyro.sample("v_obs", dist.Normal(v, v_err), obs=v_meas)

Figure

numpyro.render_model(
    model=model,
    model_args=(data,),
    render_params=True,
    render_distributions=True,
)

Figure 2: The model graph.

Sampling

sampler = numpyro.infer.MCMC(
    sampler=numpyro.infer.NUTS(model),
    num_warmup=2000,
    num_samples=10000,
    num_chains=4,
    progress_bar=False,
)

rng_key, _rng_key = jax.random.split(rng_key)
sampler.run(_rng_key, data)

inf_data = az.from_numpyro(sampler)
inf_data.posterior["sigma"] = np.exp(inf_data.posterior["log_sigma"])

Figure

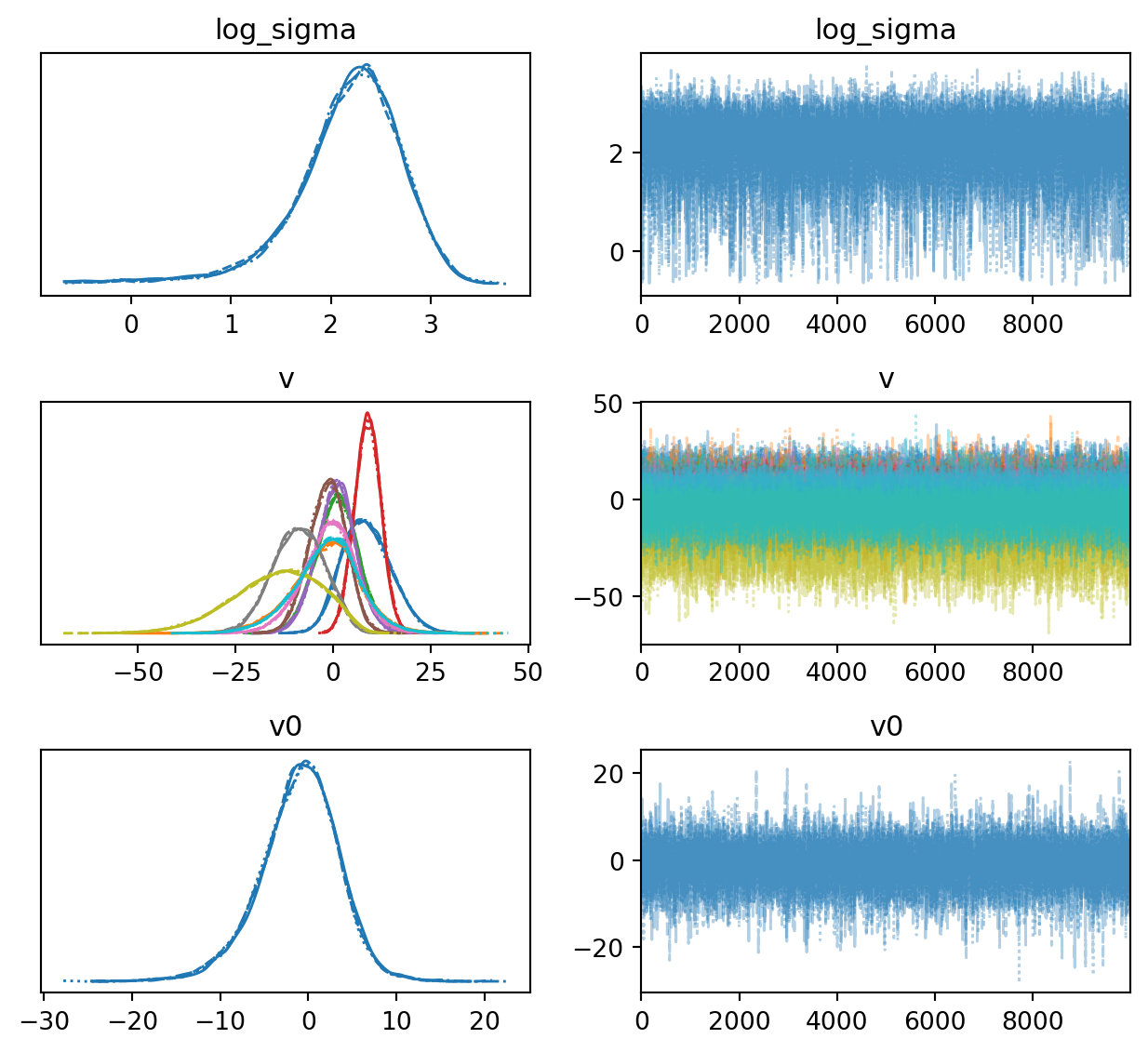
def plot_trace(ax=None):
    return az.plot_trace(
        data=inf_data,
        figsize=(FIGSIZE[0], 3 * 2),
        var_names=["~v_decentered", "~sigma"],
        axes=ax,
    )


plot_trace()
plt.tight_layout()
plt.show()

Figure 3: The MCMC trace plot.

Table

az.summary(inf_data, kind="all", var_names=["~v_decentered", "~sigma"])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
log_sigma	2.170	0.572	1.157	3.197	0.006	0.008	9047.0	10129.0	1.0
v[0]	8.650	6.255	-2.701	20.567	0.035	0.028	30636.0	30047.0	1.0
v[1]	-1.606	8.924	-19.492	14.748	0.048	0.050	35865.0	29076.0	1.0
v[2]	1.125	5.550	-9.259	11.757	0.023	0.027	59429.0	32620.0	1.0
v[3]	8.884	3.354	2.590	15.241	0.020	0.017	29404.0	22218.0	1.0
v[4]	0.739	4.978	-8.737	10.055	0.020	0.023	59184.0	33754.0	1.0
v[5]	-1.413	4.705	-10.320	7.317	0.021	0.022	49588.0	33222.0	1.0
v[6]	-0.883	7.008	-14.509	11.999	0.032	0.036	48949.0	33351.0	1.0
v[7]	-8.952	6.517	-20.825	3.281	0.042	0.030	23197.0	17708.0	1.0
v[8]	-14.822	11.393	-35.804	4.959	0.092	0.052	14216.0	17665.0	1.0
v[9]	-1.587	8.365	-18.610	13.519	0.042	0.045	39865.0	29183.0	1.0
v0	-0.992	4.513	-9.764	7.096	0.042	0.042	12883.0	12813.0	1.0

Results

Figure

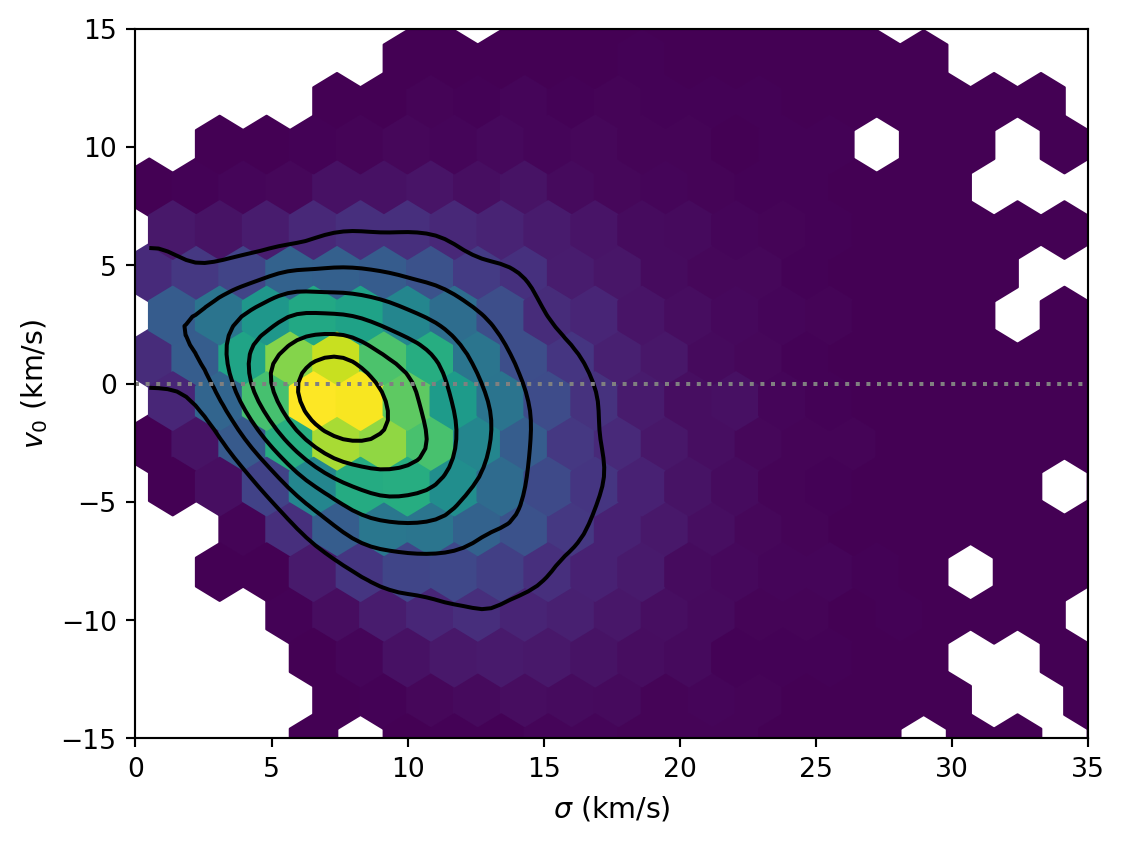
def plot_pair(ax=None):
    ax = az.plot_pair(
        data=inf_data,
        figsize=FIGSIZE,
        var_names=["sigma", "v0"],
        labeller=LABELLER,
        kind=["hexbin", "kde"],
        hexbin_kwargs={"cmap": "YlGn"},
        textsize=TEXTSIZE,
        ax=ax,
    )

    ax.axhline(0, **INDICATOR_STYLE)

    ax.set_xlim(0, 35)
    ax.set_ylim(-15, 15)
    return ax


plot_pair()
plt.show()

Figure 4: The joint posterior distribution of the velocity dispersion \(\sigma\) and the velocity offset \(v_0\).

Figure

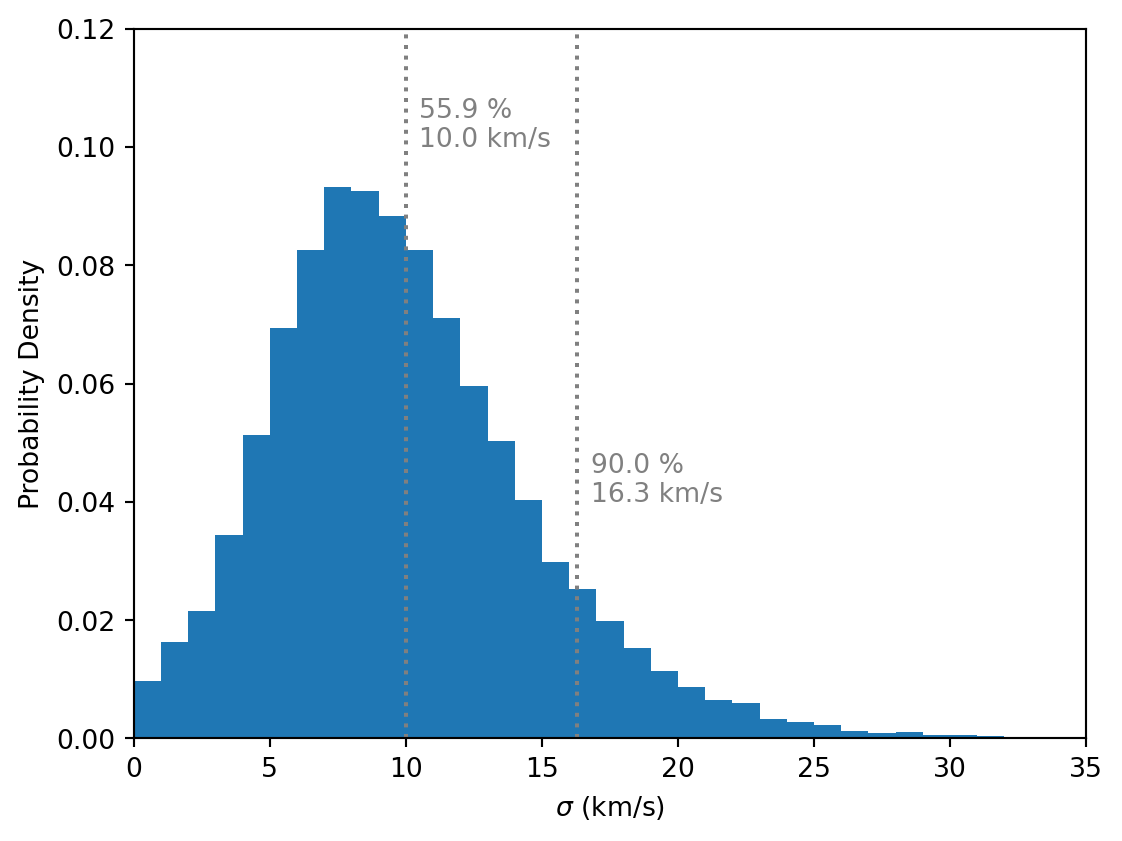
def plot_posterior(ax=None):
    if ax is None:
        _, ax = plt.subplots(figsize=FIGSIZE)

    sigma = az.extract(inf_data, var_names=["sigma"])
    ax.hist(sigma, bins=np.arange(0, 36, 1), density=True)

    for x, y, p in [
        (10, 0.1, scipy.stats.percentileofscore(sigma, 10)),
        (np.percentile(sigma, 90), 0.04, 90),
    ]:
        ax.axvline(x, **INDICATOR_STYLE)
        ax.text(x + 0.5, y + 0.005, f"{p:.1f} %", c=INDICATOR_STYLE["c"])
        ax.text(x + 0.5, y, f"{x:.1f} km/s", c=INDICATOR_STYLE["c"])

    ax.set_xlabel(r"$\sigma$ (km/s)")
    ax.set_ylabel("Probability Density")
    ax.set_xlim(0, 35)
    ax.set_ylim(0, 0.12)
    return ax


plot_posterior()
plt.show()

Figure 5: The posterior distribution of the velocity dispersion \(\sigma\).

Figure

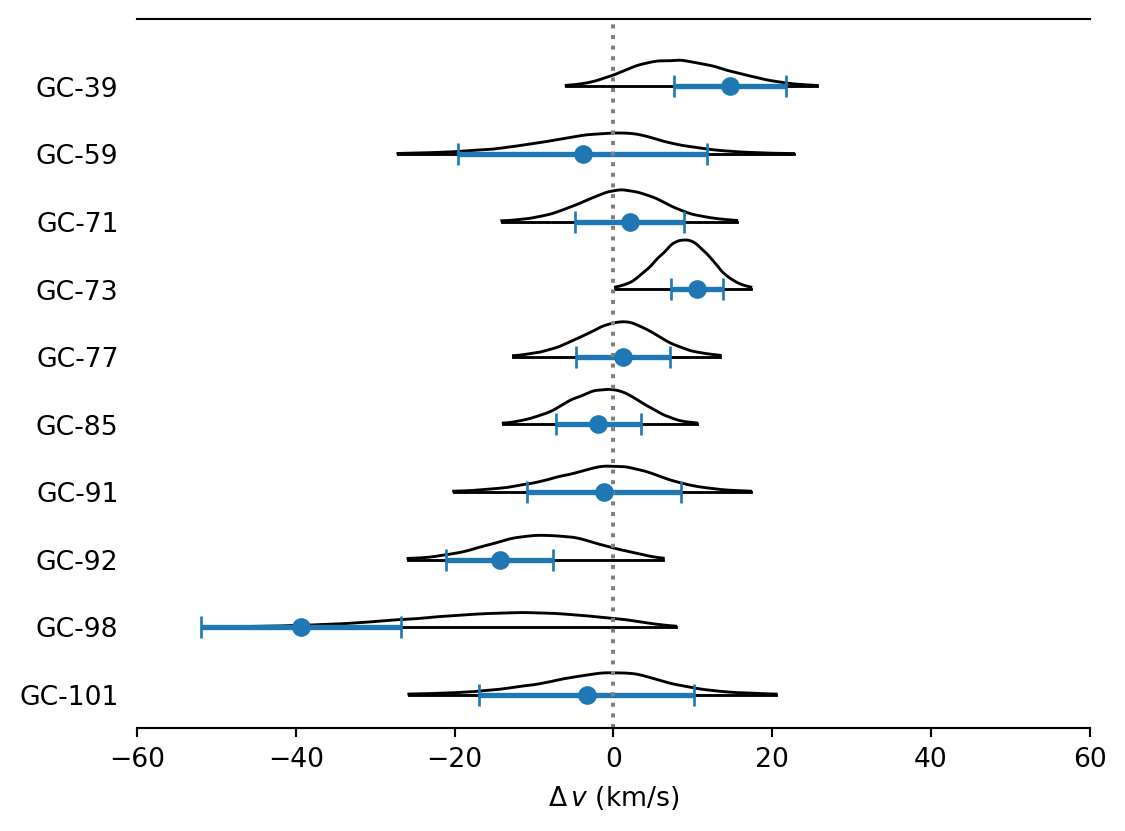
def plot_forest(ax=None):
    _ax = az.plot_forest(
        data=inf_data,
        figsize=FIGSIZE,
        var_names=["v"],
        kind="ridgeplot",
        hdi_prob=0.99,
        ridgeplot_overlap=0.6,
        ridgeplot_alpha=0,
        combined=True,
        colors="black",
        textsize=TEXTSIZE,
        ax=ax,
    )

    ax = _ax[0]
    dy = 0.825
    y = np.arange(len(data)) * dy
    y = y[::-1]

    ax.errorbar(x=data["v"], y=y, xerr=data["v_err"], **MARKER_STYLE)
    ax.axvline(0, **INDICATOR_STYLE)

    ax.set_yticks(y, labels=data["name"])
    ax.set_xlabel(r"$\Delta\,v$ (km/s)")
    ax.set_xlim(-60, 60)
    ax.set_ylim(-dy / 2, np.max(y) + dy)
    return ax


plot_forest()
plt.show()

Figure 6: The predicted velocities (black), shown together with the observed values (blue).

Resources

• A galaxy lacking dark matter (van Dokkum+ 2018)

Watermark

Python implementation: CPython
Python version       : 3.11.13
IPython version      : 9.7.0

scipy     : 1.16.3
matplotlib: 3.10.7
jax       : 0.8.0
IPython   : 9.7.0
pandas    : 2.3.3
numpy     : 2.3.4
arviz     : 0.22.0
numpyro   : 0.19.0