This notebook is part of a set of examples for teaching Bayesian inference methods and probabilistic programming, using the numpyro library.
import io
import arviz as az
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import numpyro
import numpyro.distributions as dist
import numpyro.infer
import pandas as pd
from IPython.display import display
from jax.experimental.ode import odeintFIGSIZE = (6.4, 4.8)
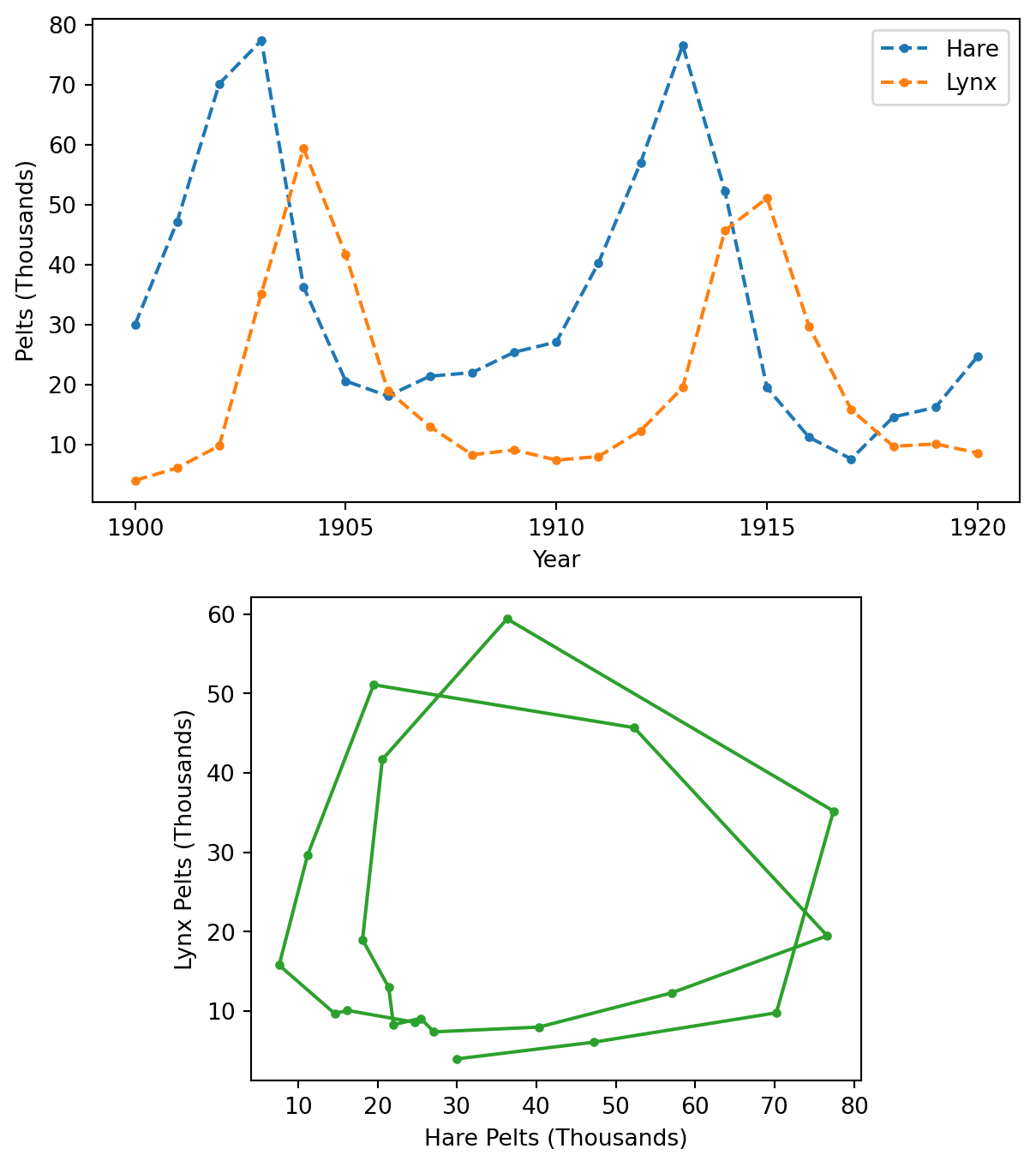
TEXTSIZE = 10rng_key = jax.random.PRNGKey(1)The data consists of the number of pelts of the Canadian lynx and the snowshoe hare collected annually between 1900 and 1920. These two species are in a predator-prey relationship, and their population sizes oscillate. In this example, we will use the Lotka-Volterra equations to model these oscillations, taking the number of collected pelts as a proxy for population size.
csv = """
year,lynx,hare
1900,4.0,30.0
1901,6.1,47.2
1902,9.8,70.2
1903,35.2,77.4
1904,59.4,36.3
1905,41.7,20.6
1906,19.0,18.1
1907,13.0,21.4
1908,8.3,22.0
1909,9.1,25.4
1910,7.4,27.1
1911,8.0,40.3
1912,12.3,57.0
1913,19.5,76.6
1914,45.7,52.3
1915,51.1,19.5
1916,29.7,11.2
1917,15.8,7.6
1918,9.7,14.6
1919,10.1,16.2
1920,8.6,24.7
"""
data = pd.read_csv(io.StringIO(csv))
data["t"] = data["year"] - data["year"].iloc[0]def plot_data_timeline(plot_kwargs=None, ax=None):
if ax is None:
_, ax = plt.subplots(figsize=FIGSIZE)
plot_kwargs = {"marker": ".", "ls": "dashed", **(plot_kwargs or {})}
data.plot(x="year", y="hare", c="C0", label="Hare", **plot_kwargs, ax=ax)
data.plot(x="year", y="lynx", c="C1", label="Lynx", **plot_kwargs, ax=ax)
ax.set_xticks(np.arange(1900, 1921, 5))
ax.set_xlabel("Year")
ax.set_ylabel("Pelts (Thousands)")
return ax
def plot_data_correlation(ax=None):
if ax is None:
_, ax = plt.subplots(figsize=FIGSIZE)
data.plot(x="hare", y="lynx", c="C2", marker=".", legend=None, ax=ax)
ax.set_xlabel("Hare Pelts (Thousands)")
ax.set_ylabel("Lynx Pelts (Thousands)")
ax.set_aspect("equal")
return ax
def plot_data(ax=None):
if ax is None:
_, ax = plt.subplots(2, 1, figsize=(FIGSIZE[0], 1.5 * FIGSIZE[1]))
plot_data_timeline(ax=ax[0])
plot_data_correlation(ax=ax[1])
return ax
plot_data()
plt.tight_layout()
plt.show()
| year | lynx | hare | t | |
|---|---|---|---|---|
| 0 | 1900 | 4.0 | 30.0 | 0 |
| 1 | 1901 | 6.1 | 47.2 | 1 |
| 2 | 1902 | 9.8 | 70.2 | 2 |
| 3 | 1903 | 35.2 | 77.4 | 3 |
| 4 | 1904 | 59.4 | 36.3 | 4 |
| 5 | 1905 | 41.7 | 20.6 | 5 |
| 6 | 1906 | 19.0 | 18.1 | 6 |
| 7 | 1907 | 13.0 | 21.4 | 7 |
| 8 | 1908 | 8.3 | 22.0 | 8 |
| 9 | 1909 | 9.1 | 25.4 | 9 |
| 10 | 1910 | 7.4 | 27.1 | 10 |
| 11 | 1911 | 8.0 | 40.3 | 11 |
| 12 | 1912 | 12.3 | 57.0 | 12 |
| 13 | 1913 | 19.5 | 76.6 | 13 |
| 14 | 1914 | 45.7 | 52.3 | 14 |
| 15 | 1915 | 51.1 | 19.5 | 15 |
| 16 | 1916 | 29.7 | 11.2 | 16 |
| 17 | 1917 | 15.8 | 7.6 | 17 |
| 18 | 1918 | 9.7 | 14.6 | 18 |
| 19 | 1919 | 10.1 | 16.2 | 19 |
| 20 | 1920 | 8.6 | 24.7 | 20 |
If \(u(t)\) is the population size of the prey species (hare) at time \(t\) and \(v(t)\) the population size of the predator species (lynx), the time evolution of \(\boldsymbol{y}_t=[u(t),v(t)]\), starting from some initial populations \(\boldsymbol{y}_0\), can be described by a pair of differential equations depending on four non-negative parameters \(\boldsymbol{\theta}=[\alpha,\beta,\gamma,\delta]\), known as the Lotka-Volterra equations:
\[\frac{d\boldsymbol{y}}{dt}=\left[\frac{du}{dt},\frac{dv}{dt}\right]=\left[(\alpha-\beta\,v)\,u,(-\gamma+\delta\,u)\,v\right]\]
def dy_dt(y, t, theta):
du_dt = (theta[..., 0] - theta[..., 1] * y[1]) * y[0]
dv_dt = (-theta[..., 2] + theta[..., 3] * y[0]) * y[1]
return jnp.stack([du_dt, dv_dt])Instead of modeling the population sizes \(\boldsymbol{y}_t\) directly, it is convenient to model the log-transformed values \(\log(\boldsymbol{y}_t)\), which are not contrained to be positive. Let’s also assume that there will be some (multiplicative) errors in measuring \(\boldsymbol{y}_t\), so that the observed population sizes \(\hat{\boldsymbol{y}}_t\) are expected to follow a log-normal distribution with standard deviation \(\boldsymbol{\sigma}\):
\[\log(\hat{\boldsymbol{y}}_t)\sim\text{Normal}(\log(\boldsymbol{z}_t),\boldsymbol{\sigma})\]
def model(df=None, t=None, ode_kwargs=None):
ode_kwargs = {"rtol": 1e-6, "atol": 1e-3, "mxstep": 1000, **(ode_kwargs or {})}
if t is None:
assert df is not None
_t = numpyro.param("t_meas", df["t"].values.astype(float))
y_meas = numpyro.param("y_meas", df[["hare", "lynx"]].values)
else:
assert df is None
_t = numpyro.param("t", t.astype(float))
y_meas = None
theta = numpyro.sample(
"theta",
dist.TruncatedNormal(
jnp.array([1.0, 0.05, 1.0, 0.05]),
jnp.array([0.5, 0.05, 0.5, 0.05]),
low=0.0,
),
)
with numpyro.plate("species", 2):
y0 = numpyro.sample("y0", dist.LogNormal(jnp.log(10), 1).expand([2]))
sigma = numpyro.sample("sigma", dist.LogNormal(-1, 1).expand([2]))
with numpyro.plate("data", len(_t)):
y = numpyro.deterministic("y", odeint(dy_dt, y0, _t, theta, **ode_kwargs))
numpyro.sample("y_obs", dist.LogNormal(jnp.log(y), sigma), obs=y_meas)numpyro.render_model(
model=model,
model_args=(data,),
render_params=True,
render_distributions=True,
)
sampler = numpyro.infer.MCMC(
sampler=numpyro.infer.NUTS(model),
num_warmup=1000,
num_samples=2000,
num_chains=4,
progress_bar=False,
)rng_key, _rng_key = jax.random.split(rng_key)
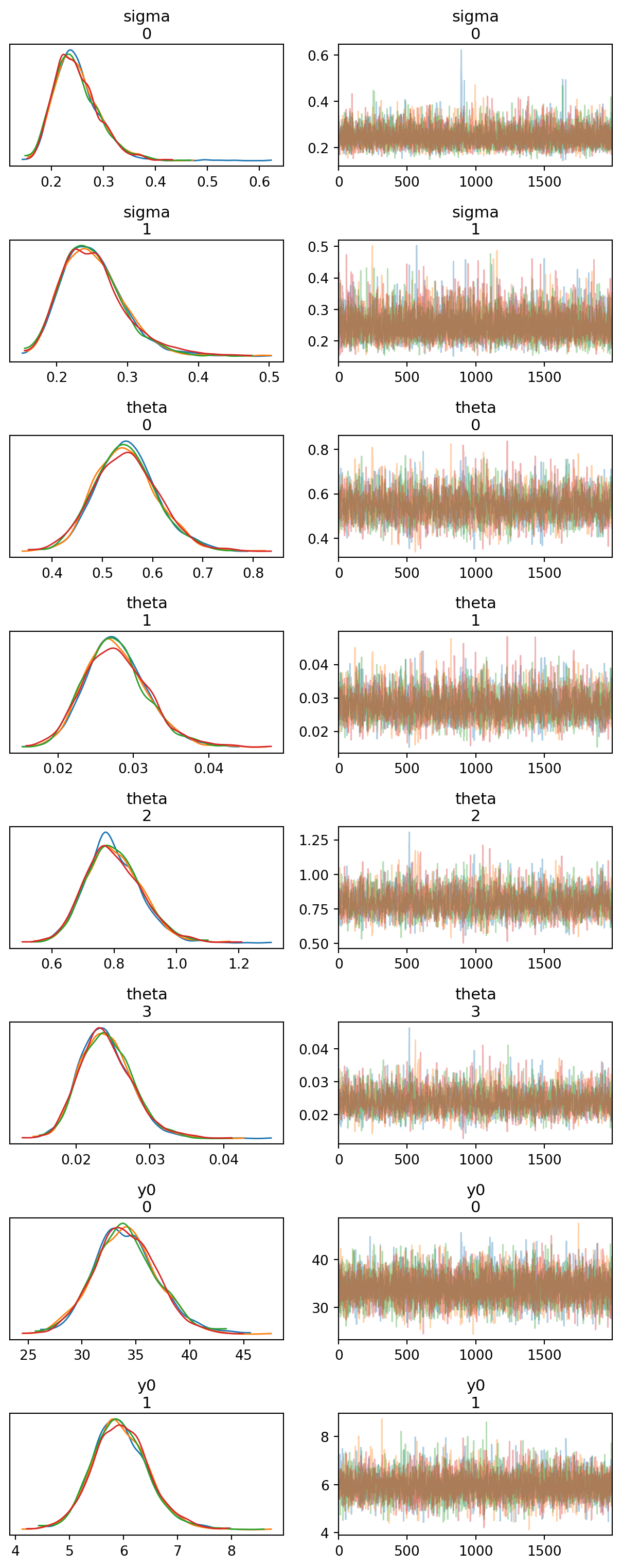
sampler.run(_rng_key, data)inf_data = az.from_numpyro(sampler)def plot_trace(ax=None):
return az.plot_trace(
data=inf_data,
figsize=(FIGSIZE[0], 8 * 2),
var_names=["~y"],
compact=False,
axes=ax,
)
plot_trace()
plt.tight_layout()
plt.show()
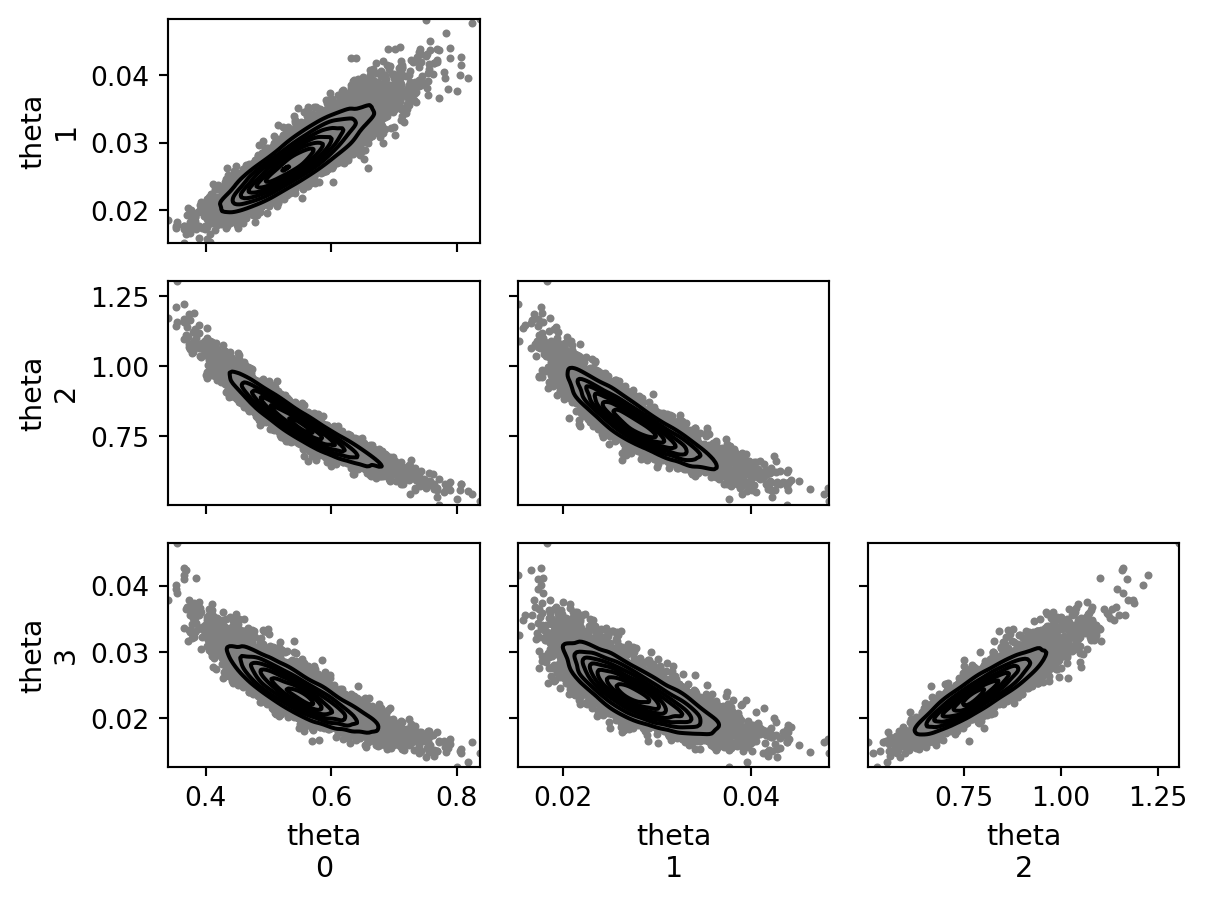
def plot_pair(ax=None):
return az.plot_pair(
data=inf_data,
figsize=FIGSIZE,
var_names=["theta"],
kind=["scatter", "kde"],
scatter_kwargs={"color": "grey"},
textsize=TEXTSIZE,
ax=ax,
)
plot_pair()
plt.tight_layout()
plt.show()
theta.az.summary(inf_data, kind="all", var_names=["~y"])| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| sigma[0] | 0.249 | 0.043 | 0.174 | 0.326 | 0.001 | 0.001 | 5214.0 | 4048.0 | 1.0 |
| sigma[1] | 0.252 | 0.045 | 0.175 | 0.335 | 0.001 | 0.000 | 5542.0 | 5131.0 | 1.0 |
| theta[0] | 0.548 | 0.064 | 0.434 | 0.672 | 0.001 | 0.001 | 1882.0 | 3019.0 | 1.0 |
| theta[1] | 0.028 | 0.004 | 0.020 | 0.036 | 0.000 | 0.000 | 1987.0 | 3194.0 | 1.0 |
| theta[2] | 0.799 | 0.090 | 0.632 | 0.966 | 0.002 | 0.002 | 1796.0 | 2810.0 | 1.0 |
| theta[3] | 0.024 | 0.004 | 0.018 | 0.031 | 0.000 | 0.000 | 1951.0 | 3112.0 | 1.0 |
| y0[0] | 34.060 | 2.948 | 28.411 | 39.491 | 0.041 | 0.029 | 5338.0 | 4242.0 | 1.0 |
| y0[1] | 5.945 | 0.524 | 4.979 | 6.949 | 0.008 | 0.006 | 4124.0 | 4545.0 | 1.0 |
predictive = numpyro.infer.Predictive(model, sampler.get_samples())
t_pred = np.linspace(0, 25, 101)
rng_key, _rng_key = jax.random.split(rng_key)
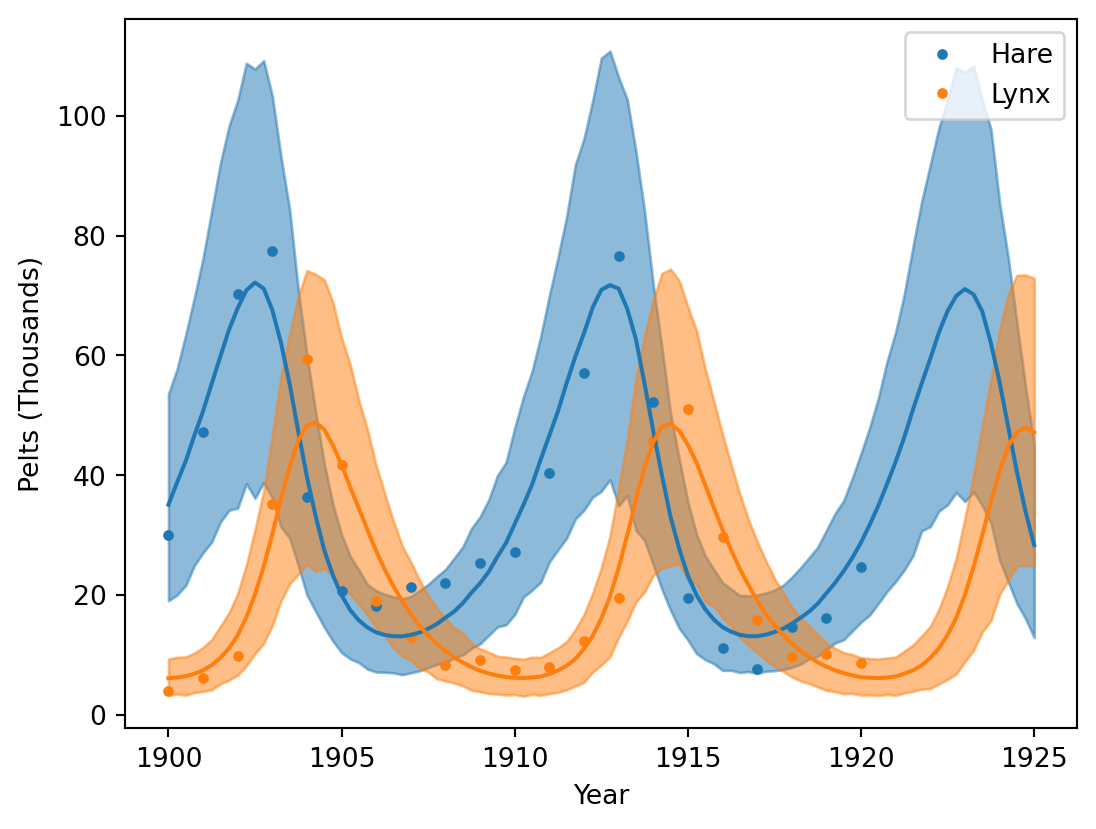
pred_data = az.from_numpyro(posterior_predictive=predictive(_rng_key, t=t_pred))def plot_pred(ax=None):
ax = plot_data_timeline(plot_kwargs={"ls": "None"}, ax=ax)
pred_mean = az.extract(pred_data, group="posterior_predictive").mean("sample")
pred_hdi = az.hdi(pred_data, group="posterior_predictive")
x = t_pred + data["year"].iloc[0]
for i in range(2):
y = pred_mean["y_obs"].sel(y_obs_dim_1=i)
ax.plot(x, y, c=f"C{i}")
y = pred_hdi["y_obs"].sel(y_obs_dim_1=i)
az.plot_hdi(x=x, hdi_data=y, color=f"C{i}", smooth=False, ax=ax)
ax.set_xticks(np.arange(1900, 1926, 5))
return ax
plot_pred()
plt.show()
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.20.0
numpy : 1.26.3
numpyro : 0.13.2
arviz : 0.17.0
matplotlib: 3.8.2
pandas : 2.1.4
jax : 0.4.23